对决深度 Q 网络

2016 年 4 月 30 日 作者：Kai Arulkumaran

深度 Q 网络 (DQN) [1] 重新燃起了人们对神经网络在强化学习中的兴趣，证明了它们在具有挑战性的街机学习环境 (ALE) 基准测试 [2] 中的能力。ALE 是一个强化学习接口，包含了超过 50 款 Atari 2600 的视频游戏；使用单一架构和超参数选择，DQN 能够在其中超过一半的游戏中取得超越人类的表现。最初的工作现在已经被多个改进所取代，其中几个可以在 GitHub 上找到。由于在 ALE 上的训练需要在 GPU 上花费超过一周的时间，该代码还设置了学习如何在 CPU 上花几个小时玩更简单的 接球 游戏。

强化学习

最近的深度学习研究主要集中在监督学习上，监督学习涉及找到从输入数据 \(x\) 到目标数据 \(y\) 的映射。具体来说，神经网络是参数化函数，\(f(x; \theta)\)，其中我们使用误差信号来学习参数 \(\theta\)。无监督学习涉及推断输入数据的结构，没有这种信号，可以用多种方法来解决（例如，聚类）。强化学习则利用奖励信号，没有明确的输入到目标数据的映射，而是以最大化接收到的奖励为目标。

在强化学习场景中，代理必须通过反复试验与环境交互来学习。正式地，我们将环境考虑为一组状态 \(\mathcal{S}\)，代理具有一组动作 \(\mathcal{A}\)。在每个离散时间步 \(t\) 中，代理观察环境的状态 \(s_t\) 并选择一个动作 \(a_t\) 来执行。然后代理会收到一个标量奖励 \(r_{t+1}\)，并观察到下一个状态 \(s_{t+1}\)。此动作-感知循环如下图所示。

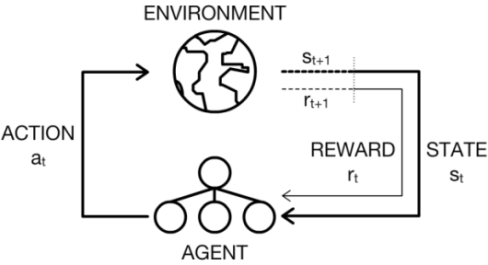
Action-perception loop

同时，代理试图学习一个（控制）策略 \(\pi\)，它用来确定在给定其当前状态的情况下应该执行哪个动作。最佳动作是在每个时间步都最大化其预期回报，\(\mathbb{E}[R]\)，其中 \(R\) 定义如下

\[R = \sum\limits_{t=0}^{T-1} \gamma^tr_{t+1}\]

在视频游戏中，\(R\) 是在一个回合（直到玩家死亡）中获得的所有奖励（分数增量）的总和，该回合持续 \(T\) 个离散时间步（通常是单个帧）。我们还使用了一个折扣变量 \(\gamma\)，它决定了代理的“远见”程度 - 值为 0 意味着代理只关心它接收到的下一个奖励，而值为 1 意味着它同样关心将来接收到的每个奖励。

解决强化学习问题的一种技术是 Q 学习，它涉及学习一个动作-价值函数

\[Q(s, a) = \mathbb{E}[R s, a]\]

如果我们可以获得最佳动作-价值函数，那么策略就变得很简单，只需根据代理所在的每个时间步的状态，选择最大化该函数的动作。但是，最佳函数对我们来说不可用，因此我们必须从经验中尝试学习它。在每个时间步中，当代理执行一个动作时，它会收到一个奖励。目标是根据误差 \(\delta\) 和学习率 \(\alpha\) 更新 \(Q\)

\[Q_{t+1}(s_t, a_t) = Q_t(s_t, a_t) + \alpha \delta\]

\(\delta\) 是 \(Q\) 的当前值与目标 \(Y\) 之间的差，目标 \(Y\) 本身是收到的奖励加上下一个状态的折扣最大 Q 值

\[\delta = \left(r_t + \gamma\max_aQ_t(s_{t+1}, a)\right) - Q_t(s_t, a_t)\]

深度 Q 网络

回到深度学习，我们可以用深度神经网络来近似 \(Q\) 而不是精确地学习它，这很有道理。事实上，神经网络过去在强化学习问题上取得了巨大成功 [3]，甚至使用了 Q 学习 [4]。因此，在玩 Atari 2600 视频游戏时，如果我们想从屏幕上的原始像素中学习 - 环境的观察到的状态 - 那么从卷积神经网络 (CNN) 开始是有意义的，这正是 DQN 所做的 [1]。我们还可以将动作的独热编码提供给神经网络，并从顶部的一个单元中获得 Q 值，但有一种更有效的方法。这是 DQN 的第一个技巧 - 它们只将屏幕作为输入，并输出顶部每个可能动作的 Q 值。这不仅减少了计算量（与对每个动作运行网络相比），而且我们预计 DQN 的较低卷积部分不会真正受到动作的影响。这样一来，较低的部分专注于提取良好的空间特征，而具有全连接层的较高部分可以更多地关注不同动作的结果。网络架构很简单

local net = nn.Sequential()
net:add(nn.View(histLen * nChannels, height, width)) -- Concatenate frames in channel dimension
net:add(nn.SpatialConvolution(histLen * nChannels, 32, 8, 8, 4, 4, 1, 1))
net:add(nn.ReLU(true))
net:add(nn.SpatialConvolution(32, 64, 4, 4, 2, 2))
net:add(nn.ReLU(true))
net:add(nn.SpatialConvolution(64, 64, 3, 3, 1, 1))
net:add(nn.ReLU(true))
net:add(nn.View(convOutputSize))
net:add(nn.Linear(convOutputSize, hiddenSize))
net:add(nn.ReLU(true))
net:add(nn.Linear(hiddenSize, m)) -- m discrete actions

DQN 训练算法的一个重要组成部分是名为经验回放 [5] 的机制。从与环境交互中获得的转换存储在经验回放内存中。然后从这些转换中进行均匀采样，以离线方式进行训练。从理论角度来说，这打破了在线学习中会影响学习的强时间相关性。从更实用的角度来看，这不仅允许数据重复使用，而且允许使用硬件高效的小批量数据。

训练算法的另一个组成部分是目标网络。强化学习中的函数近似可能不稳定，因此目标网络用于在问题中增加一些平稳性。当策略网络在行动时，缓慢更新的目标网络用于评估 \(Y\)。目标网络只包含策略网络旧版本的权重，并在大量固定步骤后更新。

可视化训练

以下论文中的一篇 [6] 使用了显著性图 [7] 的想法来查看网络关注的位置。这在强化学习环境中特别有趣，因为它为我们提供了关于代理相对于当前状态的动作的可解释性。以下视频使用引导反向传播 [8] 拍摄，以获得略微更漂亮的显著性图。

对决网络架构

在强化学习中，优势函数 [9] 可以定义如下

\[A(s, a) = Q(s, a) - V(s)\]

如果 \(Q(s, a)\) 代表在状态 \(s\) 中选择给定动作 \(a\) 的值，\(V(s)\) 代表与动作无关的状态值。此属性导致定义 \(V(s) = \max_aQ(s, a)\)。因此，\(A(s, a)\) 提供了 \(s\) 中动作效用的相对度量。对决网络架构 [6] 背后的见解是，有时动作的具体选择并不重要，因此可以更明确地对状态进行建模，与动作无关。另一个优势（并非有意）是，当在强化学习中进行自举（使用估计值进行学习）时，拥有一份良好的 \(V(s)\) 估计值会有所帮助。因此，该函数可以构建到网络的架构中（类似于 残差网络）

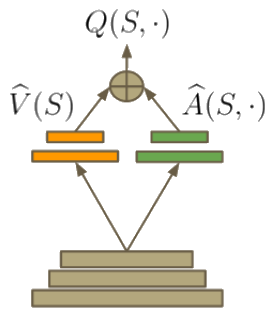
Dueling Streams

在更改 DQN 代码时，只需将顶部的全连接层替换为以下内容

-- Value approximator V^(s)
local valStream = nn.Sequential()
valStream:add(nn.Linear(convOutputSize, hiddenSize))
valStream:add(nn.ReLU(true))
valStream:add(nn.Linear(hiddenSize, 1)) -- Predicts value for state

-- Advantage approximator A^(s, a)
local advStream = nn.Sequential()
advStream:add(nn.Linear(convOutputSize, hiddenSize))
advStream:add(nn.ReLU(true))
advStream:add(nn.Linear(hiddenSize, m)) -- Predicts action-conditional advantage

-- Streams container
local streams = nn.ConcatTable()
streams:add(valStream)
streams:add(advStream)

-- Add dueling streams
net:add(streams)
-- Add dueling streams aggregator module
net:add(DuelAggregator(m))

该 聚合器模块 稍微复杂一些，但可以使用 Torch 的标准表容器构建。

训练

如前所述，在 ALE 上的训练可能需要超过一周才能完成。对于更快的测试，Pong 是一个很好的游戏，因为它应该在大约正常的训练迭代次数的十分之一（通常在 GPU 上运行一天）内取得完美或接近完美的结果。对于那些想要看到更直接结果的人来说，该代码还设置了玩 Catch - 一个 24\(\times\)24px 黑白环境，其中底部代理的球拍必须接住掉落的球。

结果

下面我们可以看到原始 DQN、双 DQN (DDQN) [10]（它使用 Q 学习更新规则的改进版本）和对决 DQN 在太空侵略者中的区别。与原始论文一样，对决 DQN 也使用与 DDQN 相同的更新规则。

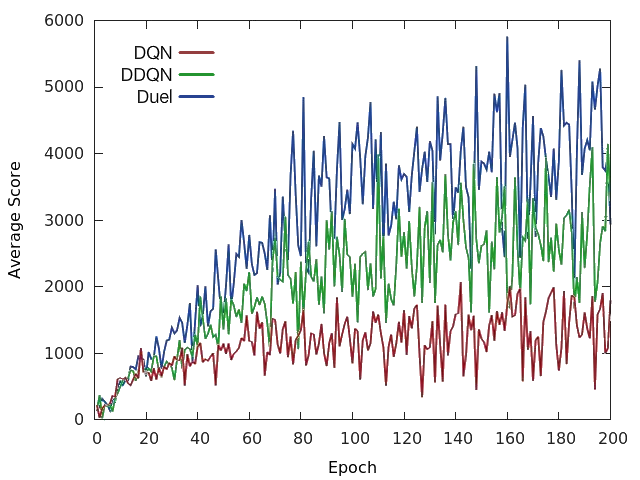
Scores of DQN, DDQN and Dueling DQN on Space Invaders

总的来说，对决网络架构在几乎所有游戏中都比原始 DQN 和 DDQN 取得了更好的性能 [6]。更重要的是，这个概念可以与 DQN 上的其他改进结合使用，这意味着它可以用作成功的深度强化学习代理的一个组成部分。

结论

本文讨论了 DQN 如何能够在高维视觉域中学习成功的策略，以及如何通过纯粹的架构添加来使其更强大。它还研究了如何使用 CNN 可视化技术来理解 DQN 的动作。

鸣谢

DeepMind 发布了他们的源代码 [1]，它被用作参考。
Laszlo Keri 和 代码库 的其他贡献者。

参考资料

  1. Mnih, V., Kavukcuoglu, K., Silver, D., Rusu, A. A., Veness, J., Bellemare, M. G., … & Petersen, S. (2015). 通过深度强化学习实现人类级别的控制。自然，518(7540), 529-533.
  2. Bellemare, M. G., Naddaf, Y., Veness, J., & Bowling, M. (2013). 街机学习环境：一般代理的评估平台。人工智能研究杂志，47, 253-279.
  3. Tesauro, G. (1994). TD-Gammon，一个自学西洋双陆棋程序，达到大师级水平。神经计算，6(2), 215-219.
  4. Riedmiller, M. (2005). 神经拟合 Q 迭代 - 数据高效神经强化学习方法的首次体验。在机器学习：ECML 2005（第 317-328 页）。施普林格柏林海德堡。
  5. Lin, L. J. (1992). 基于强化学习、规划和教学的自学习反应式代理。机器学习，8(3-4), 293-321.
  6. Wang, Z., de Freitas, N., & Lanctot, M. (2015). 用于深度强化学习的对决网络架构。arXiv 预印本 arXiv:1511.06581.
  7. Simonyan, K., Vedaldi, A., & Zisserman, A. (2013). 深入卷积网络：可视化图像分类模型和显著性图。arXiv 预印本 arXiv:1312.6034.
  8. Springenberg, J. T., Dosovitskiy, A., Brox, T., & Riedmiller, M. (2014). 追求简单：全卷积网络。arXiv 预印本 arXiv:1412.6806.
  9. Baird III, L. C. (1993). 优势更新（第 WL-TR-93-1146 号）。赖特实验室赖特-帕特森空军基地俄亥俄州。
  10. Van Hasselt, H., Guez, A., & Silver, D. (2015). 使用双重 Q 学习的深度强化学习。arXiv 预印本 arXiv:1509.06461.
由 Disqus 提供支持的评论